Вертикальный план
На вертикальном плане, называемом также продольным разрезом, изображается прохождение по высоте проезжей части дороги (рис. 1). Основной линией является трассированная на генеральном плане ось. Вдоль этой линии площадка режется по вертикали. На пунктах станций указываются высоты существующей площадки, которые беруться либо из планов, или их получают путем измерений на местности. Длина основной линии и ее отрезков откладывается в масштабе генерального плана, например 1:500. Высоты изображаются в 10 раз большем масштабе. Это необходимо, чтобы перепады высот на чертеже были заметными. Высоты относятся к свободно выбираемому относительному горизонту, в большинстве — относительно нормального нуля (рис. 1).
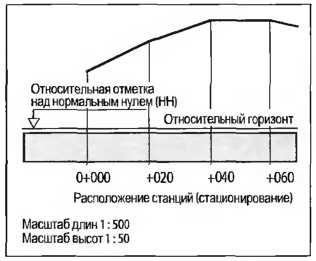
Рис. 1. Представление высот площадки на вертикальном плане
Продольные уклоны, выпуклости, вогнутости
Вертикальная планировка проезжей части получается сначала графически, потом — расчетным путем. Полученную линию называют градиентом (рис. 2). Она состоит из последовательности прямых идут окружностей. Продольные уклоны прямых задаются в процентах. При графическом построении градиента учитываются существующие обязательные высотные точки, например другие транспортные дороги, мосты, подъезды и водоводы. Подъемы с большим продольным уклоном создают препятствия для транспортного потока, особенно для большегрузных автомобилей. Поэтому нельзя превышать определенные предельные продольные уклоны (табл. 1). Для дорог с большой транспортной нагрузкой необходимо проверить, не появится ли необходимость прокладки дополнительной полосы на отрезке подъема.
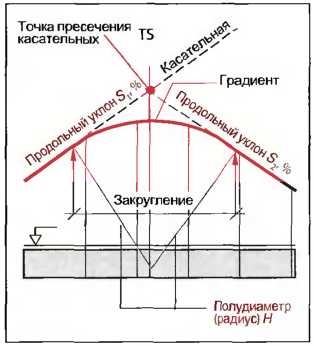
Рис. 2. Градиент
| Таблица 1. Наибольшие продольные уклоны, радиусы закругления горок и ванн по RAS-L | ||||
| ve, км/ч | Наибольший продольный уклон макс. s, % для дорог категории: | Минимальный радиус закругления горок Нк, м | Рекомендуемый минимальный радиус закруглений в выемках Нw, м | |
| А | BI/BII | |||
| 50 | 9,0 | 12,0 | 1400 | 500 |
| 60 | 8,0 | 10,0 | 2400 | 750 |
| 70 | 7,0 | 8,0 | 3150 | 1000 |
| 80 | 6,0 | 7,0 | 4400 | 1300 |
| 90 | 5,0 | 6,0 | 5700 | 2400 |
| 100 | 4,5 | 5,0 | 8300 | 3800 |
| 120 | 4,0 | - | 16 000 | 8800 |
Прямые с различными продольными уклонами разрезаются пересечением касательных (TS). Различают перемену наклона и смену уклонов (рис. 3). Градиент необходимо закруглить в точках пересечения касательных. При этом получается либо выпуклая, либо вогнутая часть дороги с радиусом (полудиаметром) закругления Н. В основном радиусы закругления выбираются такими большими, как это только возможно, определенные минимальные радиусы закругления должны быть соблюдены (табл. 1). В случае выпуклостей или горок это имеет особое значение, так как при уменьшающихся радиусах выпуклостей снижается дальность обзора для водителей и препятствия на проезжей части становятся видными слишком поздно.
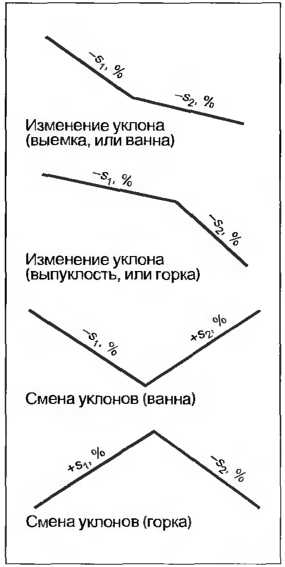
Рис. 3. Смена уклонов, изменение уклона
Расчет высотных отметок градиента
После произведенного графического изображения градиента и точек пересечения касательных следует расчетное определение высотных отметок градиента и получение вертикального плана (рис. 4).
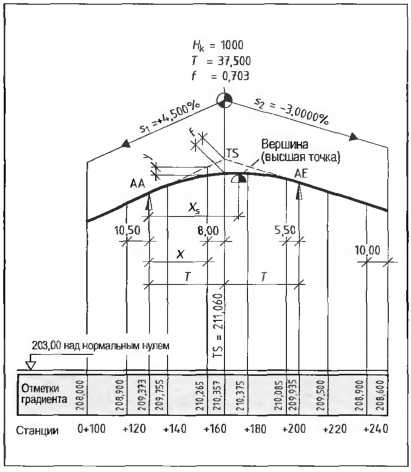
Рис. 4. Вертикальный план
Обозначения:
- Подъем: положительный (+s1, +s2);
- Спуск: отрицательный (-s1, —s2);
- Радиус ванны (Hw): положительный (+Н);
- Радиус горки (Нk): отрицательный (-H);
- Н — радиус дуги окружности, м;
- Т — длина касательной, м;
- s1, s2 — продольные уклоны касательных, %;
- Xs — абсцисса вершины горки или выемки;
- f — расстояние от точки пересечения касательных до вершины дуги;
- s — вершина душ;
- TS — точка пересечения касательных;
- АА — начало закругления;
- АЕ — конец закругления;
- Т — длина касательных приданном радиусе закругления;
- х — ордината любой точки;
- у — расстояние от дуги до касательной в любой точке.
Расчет градиента:
- Продольный уклон S, %
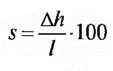 Δh — перепад высот, l — длина между точками пересечения касательных
Δh — перепад высот, l — длина между точками пересечения касательных - Длина касательной Г, м
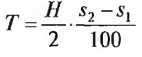 Учитывать условные обозначения!
Учитывать условные обозначения! - Расстояние между точкой пересечения касательных и вершиной дуги (штихмас)f, м
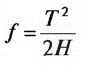
- Положение вершины
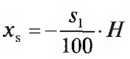 Учитывать условные обозначения!
Учитывать условные обозначения! - Высотные отметки касательных на любом месте
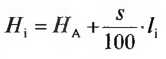 НА — высота точки пересечения касательных, li — расстояние от точки пересечения касательных
НА — высота точки пересечения касательных, li — расстояние от точки пересечения касательных - Штихмас у, м
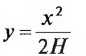 Учитывать условные обозначения!
Учитывать условные обозначения!
Пример: расчет высотных отметок градиента Нс для станций 0+160 (рис. 4):

Полоса кривизны
При проектировании градиента и поперечных уклонов необходимо учитывать распределение кривизны оси дороги, которое изображается в виде полосы кривизны (рис. 5). Расстояние линии кривизны от относительной оси рассчитывается математически.
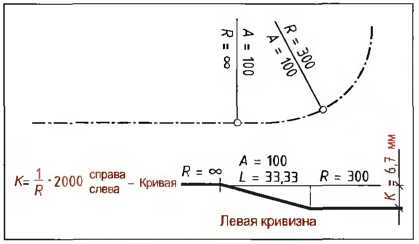
Рис. 5. Полоса кривизны
Чем меньше радиус оси проезжей части, тем больше расстояние К до относительной оси. Коэффициент п необходимо выбирать таким образом, чтобы было возможно наглядное представление полосы кривизны. Однако он должен быть одинаковым д ля всей полосы кривизны в целом. Если элементом проезжей части является прямая, то радиус R = ∞ и расстояние К= 0. Правые кривые изображаются сверху, левые — снизу от относительной оси.

Полоса поперечных уклонов
На полосе поперечных уклонов изображаются высоты краев проезжей части относительно оси проезжей части дороги. Поперечный уклон необходим для отведения поверхностной воды. На поперечных уклонах частично снимается также центростремительная сила, возникающая при движении по кривой. Минимальный поперечный уклон на прямых и на окружностях дуги составляет:
мин. q = 2,5%.
На дорогах категории А и В предусматриваются односторонние поперечные уклоны, тогда как на других дорогах может быть выбран двускатный профиль (рис. 6). Максимальный поперечный уклон проезжей части составляет:
мин. q= 8,0%.
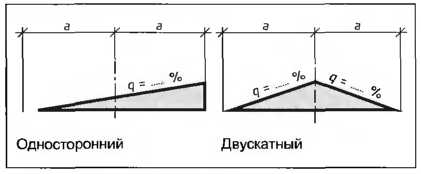
Рис. 6. Поперечные уклоны
Поперечные уклоны рассчитываются взависимостиотрадиуса кривых (рис. 7). Пример: При категории дороги A, v85 = 70 км/ч и R = 300 м поперечный уклон составляет q = 4,8%.
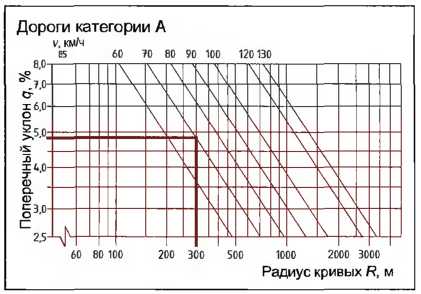
Рис. 7. Поперечные уклоны по RAS-L
Для предотвращения соскальзывания автомобиля при гололеде результирующий косой уклон может быть рассчитан по теореме Пифагора.
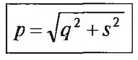
Полоса поперечных уклонов показывается на вертикальном плане под полосой кривизны. Перепады высот Δh между осью проезжей части и ее краями рассчитываются с учетом ширины дороги и поперечных уклонов.
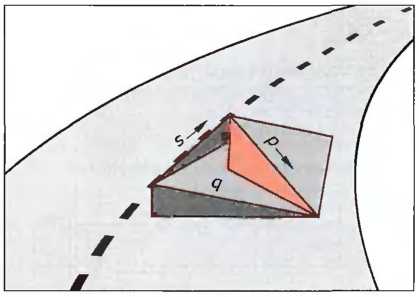
Рис. 8. Косой уклон дороги
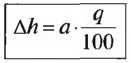
а — расстояние края дороги от оси.
Рассчитанные перепады высот откладываются в любом масштабе, например в масштабе L: 10 от основной оси. Правый и левый края дороги изображаются различными видами линий (рис. 9).

Рис. 9. Поперечные уклоны в переходных зонах
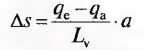
- s — уклон подгонки рампы, %;
- qe — поперечный уклон в конце участка скручивания, %;
- qа — поперечный уклон в начале участка скручивания. qа следует считать отрицательным, если он направлен противоположно qe;
- Lv — длина участка перехода, м;
- а — расстояние края проезжей части от ее оси, м.
Подгонка поперечных уклонов производится на переходном отрезке, в случае дорог категории А она производится на клотоиде. При этом плоскость проезжей части в соответствии с подгоняемым уклоном поворачивается вокруг ее оси, т.е. имеет место скручивание. Высоты краев проезжей части изменяются по отношению к ее оси; это изменение называют подгонкой рампы. При этом из оптических соображений, а также из соображений динамики движения следует придерживаться определенных граничных значений (табл. 2).
| Таблица 2. Граничные значения уклонов подгонки рампы | |||
| ve, км/ч | Макс. Δs, % при: | Мин. Δs, % | |
| а < 4,00 м | а ≥ 4,00 м | ||
| 50 | 0,50*а | 2,0 | |
| 60...70 | 0,40*а | 1,6 | 0,10*а |
| 80...90 | 0,25*а | 1,0 | (≤ макс. Δs) |
| 100...120 | 0,225*а | 0,9 | |
При скручивании между противоположными поперечными уклонами в одном месте поперечный уклон составляет 0%. В этом месте следует обращать внимание на то, чтобы проезжая часть имела продольный уклон не менее 0,5%, так как в противном случае выпадающая на поверхность дождевая вода не сможет стекать с проезжей части (рис. 10).
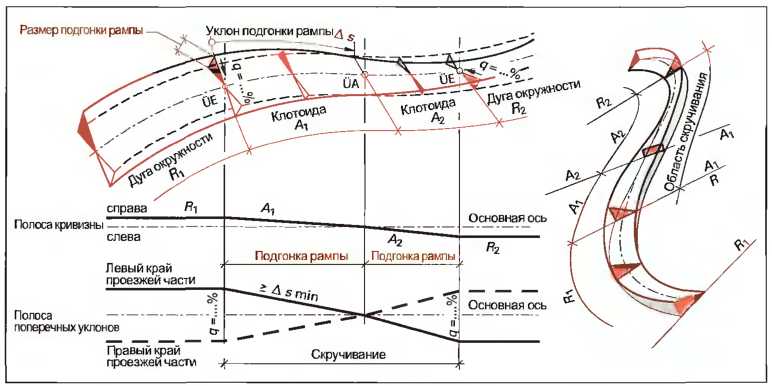
Рис. 10. Подгонка рампы и скручивание при линии дороги с перегибом
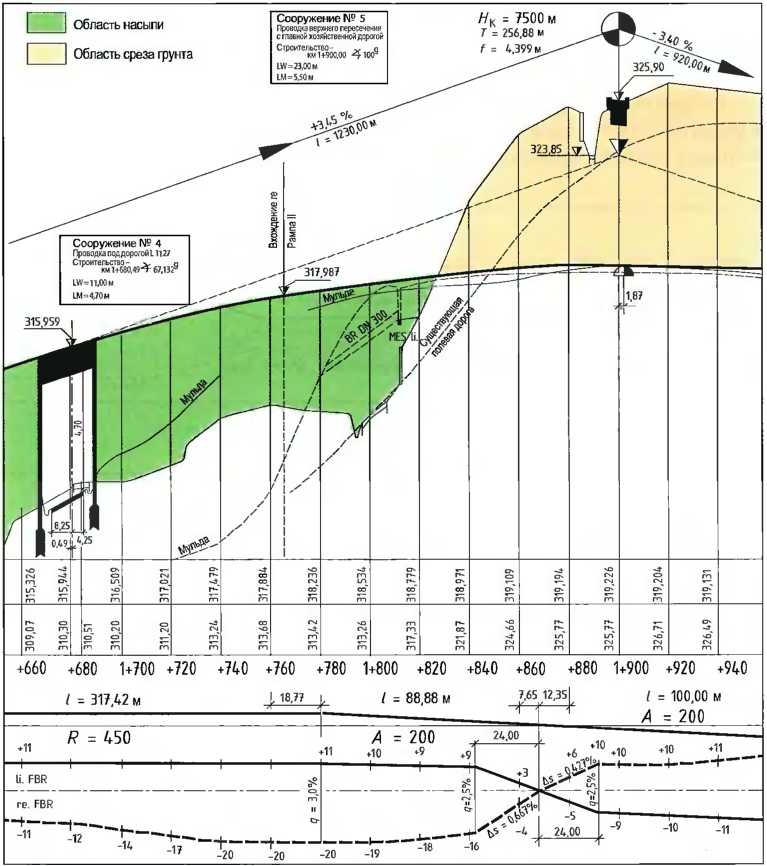
Рис. 11. Фрагмент вертикального плана
