Генеральный план
Элементы трассы на генеральном плане — это прямые, дуги окружностей и переходные кривые (рис. 11).
Прямые
Простейшим и кратчайшим соединением двух точек является прямая. Она может иметь преимущество в качестве проектного элемента, например на равнине или в длинных долинах (рис. 1). Недостатком длинных прямых дорог является то, что они способствуют развитию высокой скорости, что затрудняет оценку расстояний и скоростей других автомобилей, а также повышенная опасность ослепления ночью. Кроме того, прямые дороги трудно вписываются в холмистый ландшафт.
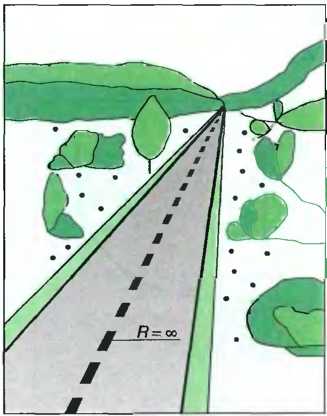
Рис. 1. Прямая
Дуги окружностей
Для того чтобы получить линию, более подходящую к данному ландшафту и к топографическим условиям местности, при проектировании дорог применяются дуги окружностей (рис. 2). Кривизна дуги окружности определяется радиусом R. При трассировке свободных отрезков из соображений динамики движения необходимо выбирать по возможности больший радиус. С другой стороны, радиусы должны выбираться только такой величины, чтобы проектируемая трасса гармонично вписывалась в ландшафт. Часто существующие условия, например существующие здания или другие транспортные пути, не допускают выбора больших радиусов закругления. Но из соображений динамики движения при трассировке свободных участков нельзя принимать радиусы меньше определенных минимальных значений (табл. 1). Минимальные радиусы зависят от проектной скорости ve. Для того чтобы радиусы можно было изобразить на генплане, применяют дуговые линейки (рис. 3).
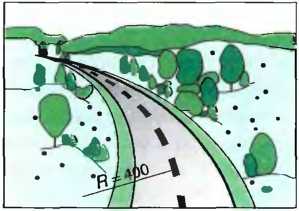
Рис. 2. Дуга окружности
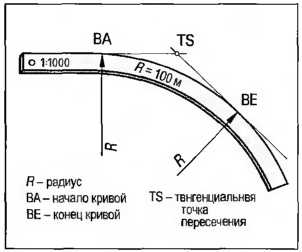
Рис. 3. Дуговая линейка
| Таблица 1. Минимальные радиусы кривых и минимальные параметры клотоиды по RAS-L | ||
| vе, км/ч | Мин. R, м | Мин. А, м |
| 50 | 80 | 30 |
| 60 | 120 | 40 |
| 70 | 180 | 60 |
| 80 | 250 | 80 |
| 90 | 340 | 110 |
| 100 | 450 | 150 (120) |
| 120 | 720 | 240 (120) |
| (...) величина в виде исключения | ||
Приведенный на дуговой линейке радиус относится к изображению в масштабе 1:1000. Поэтому при трассировке в других масштабах требуется пересчет. Если, например, необходимо чертить по линейке радиусом R = 200 в масштабе 1:500, то следует выбирать дуговую линейку с радиусом R = 400.
Переходные кривые
При езде на автомобиле по прямой дороге руль можно не поворачивать. То же самое относится при езде по дуге окружности. В местах переходов от прямых к дугам необходимо произвести обратный поворот руля. При этом действующие при движении по окружности силы (центробежные силы) вступают в действие мгновенно. Чтобы этого избежать и обеспечить возможность плавного поворота руля между прямыми и дугами окружности предусматриваются переходные кривые. Их называют клотоидами. На длине переходной кривой происходит изменение радиуса закругления. Одновременно на длине переходной кривой предпринимается изменение поперечного уклона проезжей части. С помощью применения переходных кривых обеспечивается непрерывность линии проезжей части, которая позволяет двигаться с равномерной скоростью и дает оптически непрерывную (плавную) линию дороги. Переходные кривые в дорожном строительстве образуются как клотоиды. При такой спиралеобразной кривой кривизна обратно пропорциональна длине дуги. Тем не менее применяется в качестве переходной кривой только плоская часть в начале клотоиды (рис. 4).

Рис. 4. Клотоида
Закон образования клотоиды гласит: А2 = R*L
- А — параметр клотоиды
- R — радиус, м
- L — длина клотоиды между началом и концом переходной дуги, м
Величина клотоиды определяется параметром клотоиды (А). Он является коэффициентом увеличения клотоиды (рис. 5).
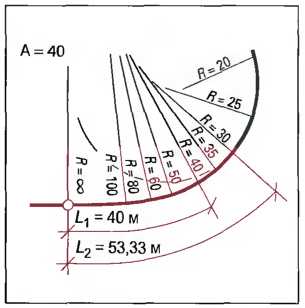
Рис. 5. Клотоида как переходная кривая
Величины, необходимые для получения клотоиды принимаются либо по таблице клотоид (табл. 2), либо могут быть получены по формулам (рис. 6).
| Таблица 2. Фрагмент таблицы клотоид | |||||||||
| Элементы построения клотоид при параметре А = 100 | |||||||||
| L | τgon | R | ΔR | XM | X | Y | Тк | ТL | L |
| 100,000 | 31,8310 | 100 | 4,130 | 49,586 | 97,529 | 16,371 | 34,148 | 67,561 | 100,000 |
| 111,111 | 39,2975 | 90 | 5,638 | 54,857 | 106,951 | 22,248 | 38,436 | 75,609 | 111,111 |
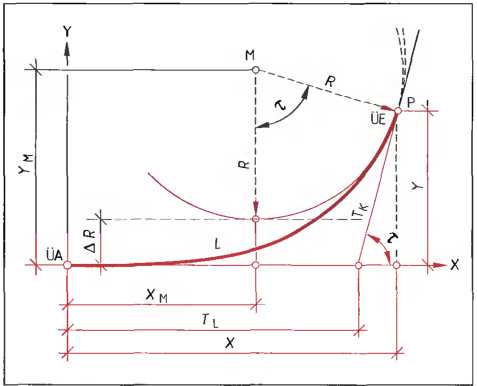
Рис. 6. Элементы построения клотоиды
Выбранные параметры клотоиды должны находиться в определенном соотношении друг к другу. Так параметр клотоиды должен составлять не менее R/3, однако не должен быть больше радиуса R.
Как и для дуг окружностей, выбор параметров клотоиды зависит от проектной скорости (табл. 1). При проектировании дорог применяются следующие формулы переходных кривых:
- простая клотоида как переход от прямой к дуге окружности;
- поворотная клотоида как переход между двумя дугами, обратно выгнутыми по отношению друг к другу;
- яйцеобразная клотоида как переход между одинаково выгнутыми дугами разного радиуса (рис. 7).
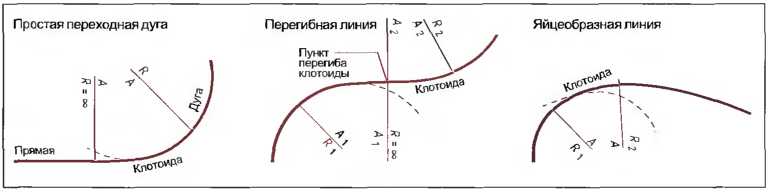
Рис. 7. Возможности применения клотоид
Для изображения клотоиды на чертеже применяются клотоидные линейки (рис. 10).
Нанесенный на клотоидную линейку параметр относится к масштабу 1:1000. Как и в дуговых линейках необходим пересчет в соответствующий масштаб.
Часто встречающейся задачей при проектировании дорог является построение дуги окружности, включая переходную кривую между двумя заданными прямыми (рис. 8).
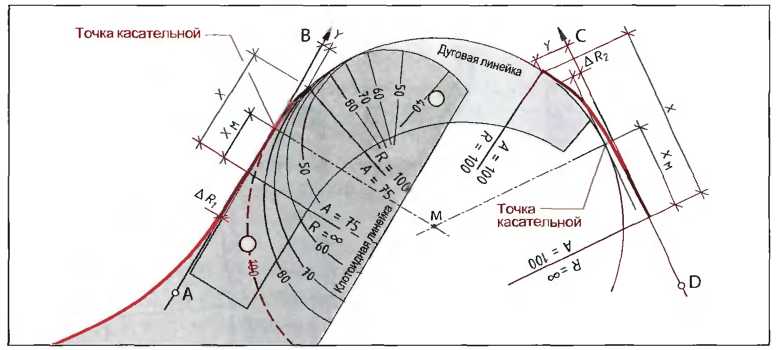
Рис. 8. Применение клотоид (пример)

- R — радиус дуги, полудиаметр закругления, м;
- Хм, Ум — координаты центра закругления радиуса в точке Р;
- М — центр закругления;
- L — длина клотоиды от начальной точки до пункта Р;
- X, Y — координаты точки Р;
- ΔR — тангенциальное уменьшение радиуса R в точке Р;
- UA,UE — начало переходной кривой, конец переходной кривой;
- ТK, TL — короткий и длинный тангенсы;
- τgon — угол между тангенсами в точке клотоиды в гонах.
Пример:
Направления прямых АВ и CD, дуга окружности с радиусом R = 100 м.
Параметры клотоиды A1 = 75 и А2= 100.
Решение: ΔR принимаем по таблице клотоид, на расстоянии ΔR1, и ΔR2 вычерчиваются параллельные линии к прямым АВ и CD, с помощью дуговых линеек между параллельными линиями встраивается дуга окружности радиусом R = 100 м и отмечаются точки касания касательных. Значения Xм, Х и Y берутся по таблице клотоид и откладываются на чертеж. Затем накладывается клотоидная линейка. При этом основные касательные клотоиды должны накрыть прямые АВ и CD. Одновременно нанесенный на клотоидную линейку радиус R = 100 м должен по положению совпасть с конструируемым радиусом окружности R = 100 м. После этого вычерчивается переходная кривая.
Если ось дороги на всем участке строительства трассирована, она может быть рассчитана с помощью соответствующей программы. Для этого необходимо задать трассирующие элементы и их координаты. Результаты расчета выдадут основные точки оси дороги. Ими являются те места оси, где происходит смета элементов. Далее можно рассчитать мелкие точки на оси. Это — точки станций на оси (рис. 9). Теперь главные точки оси могут быть перенесены на карту. Ось изображается штрихпунктирной линией. На мелких точках оси наносятся направления поперечных профилей в виде перпендикуляров к касательным к оси в этих точках. В районе дуги окружности конструируют радиальное направление с помощью циркуля, в области клотоиды нанесенные на нее направления служат в качестве вспомогательных линий для указания радиусов (рис. 10). По вычисленным координатам главных и мелких точек оси она может быть разбита на местности.
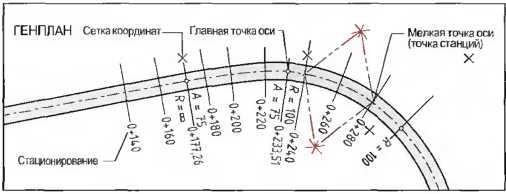
Рис. 9. Представление оси на генплане
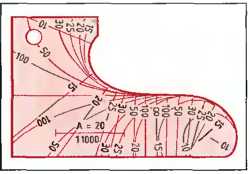
Рис. 10. Клотоидная линейка
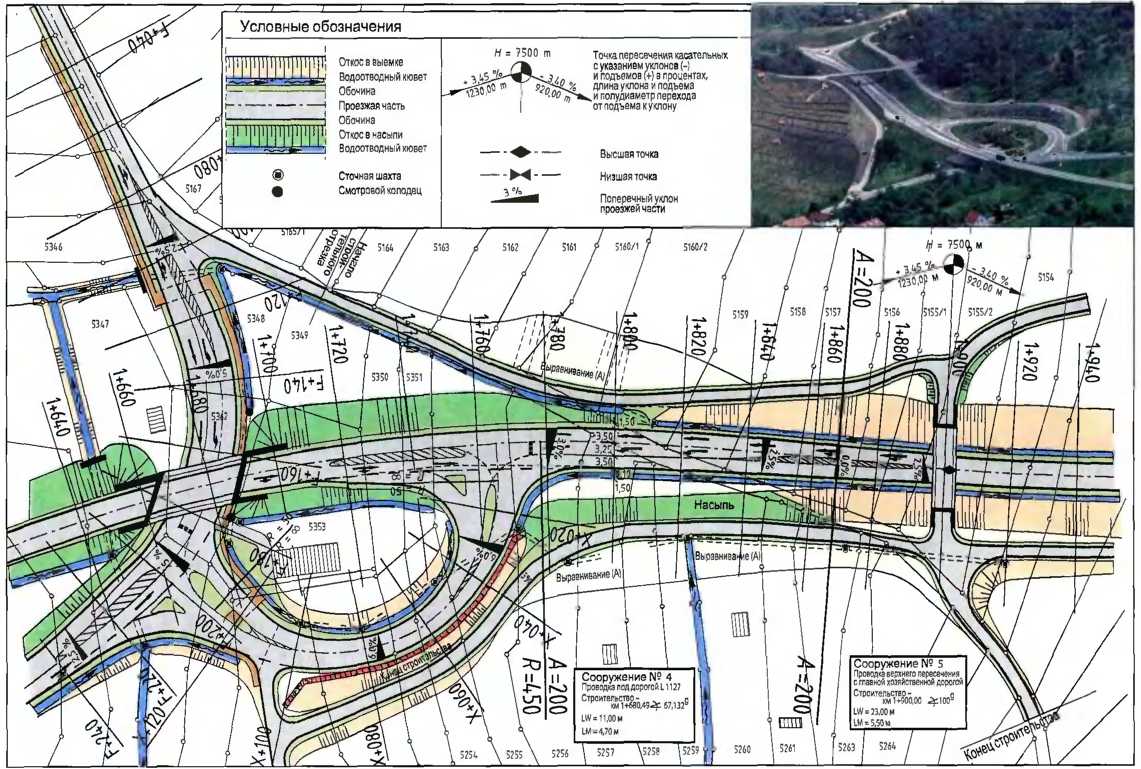
Рис. 11. Фрагмент генплана
